 [1]
[1]
Math notation works with our limited attention by greatly compressing information
…human brains, though exceedingly complex, are only able to concentrate consciously on a few things at once, requiring a mechanism to cope with the complication:
- “…early processing is largely parallel – a lot of different activities proceed simultaneously. Then there appear to be one or more stages where there is a bottleneck in information processing. Only one (or a few) ‘object(s)’ can be dealt with at a time. This is done by temporarily filtering out the information coming from the unattended objects. The attentional system then moves fairly rapidly to the next object, and so on, so that attention is largely serial (i.e., attending to one object after another) not highly parallel (as it would be if the system attended to many things at once).”
- “Mathematics is amazingly compressible: you may struggle a long time, step by step, to work through some process or idea from several approaches. But once you really understand it and have the mental perspective to see it as a whole, there is often a tremendous mental compression. You can file it away, recall it quickly and completely when you need it, and use it as just one step in some other mental process. The insight that goes with this compression is one of the real joys of mathematics.”[2]
Math notation works by being a pointer to both data and procedures at the same time
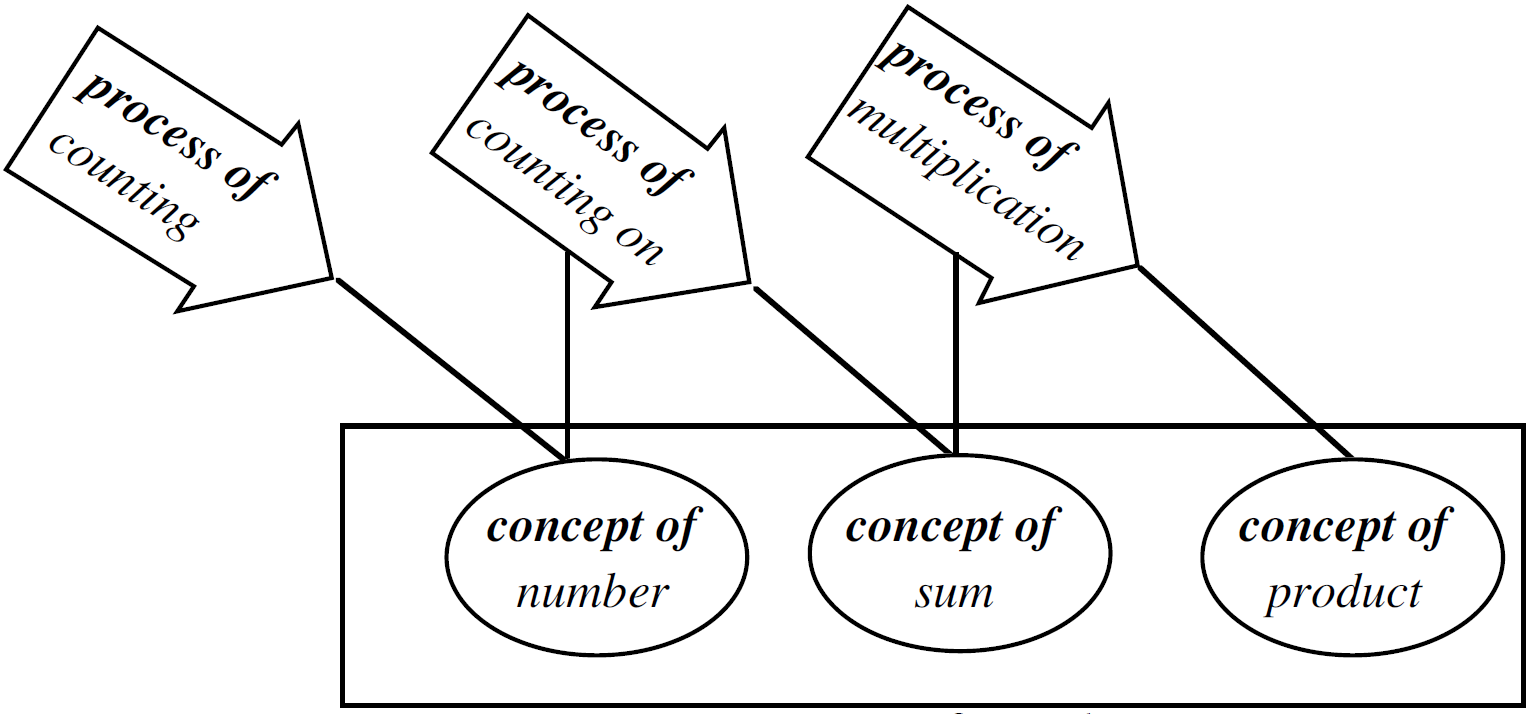
…process and concept are combined in a single notion… in the working practices of professional mathematicians and all those who are successful in mathematics. They employ the simple device of using the same notation to represent both a process and the product of that process:
- The symbol 5+4 represents both the process of adding through counting all or counting on and the concept of sum (5+4 is 9).
- The symbol 4×3 stands for the process of repeated addition “four multiplied by three” which must be carried out to produce the product of four and three which is the number 12.
- The algebraic symbol 3x+2 stands both for the process “add three times x and two” and for the product of that process, the expression “3x+2”.[1]
- Gray, Eddie M., and David O. Tall. “Duality, ambiguity, and flexibility: A ‘proceptual’ view of simple arithmetic.” Journal for Research in Mathematics Education 25.2 (1994): 116-140.
- Gray, Eddie, and David Tall. “Abstraction as a natural process of mental compression.” Mathematics Education Research Journal 19.2 (2007): 23-40.