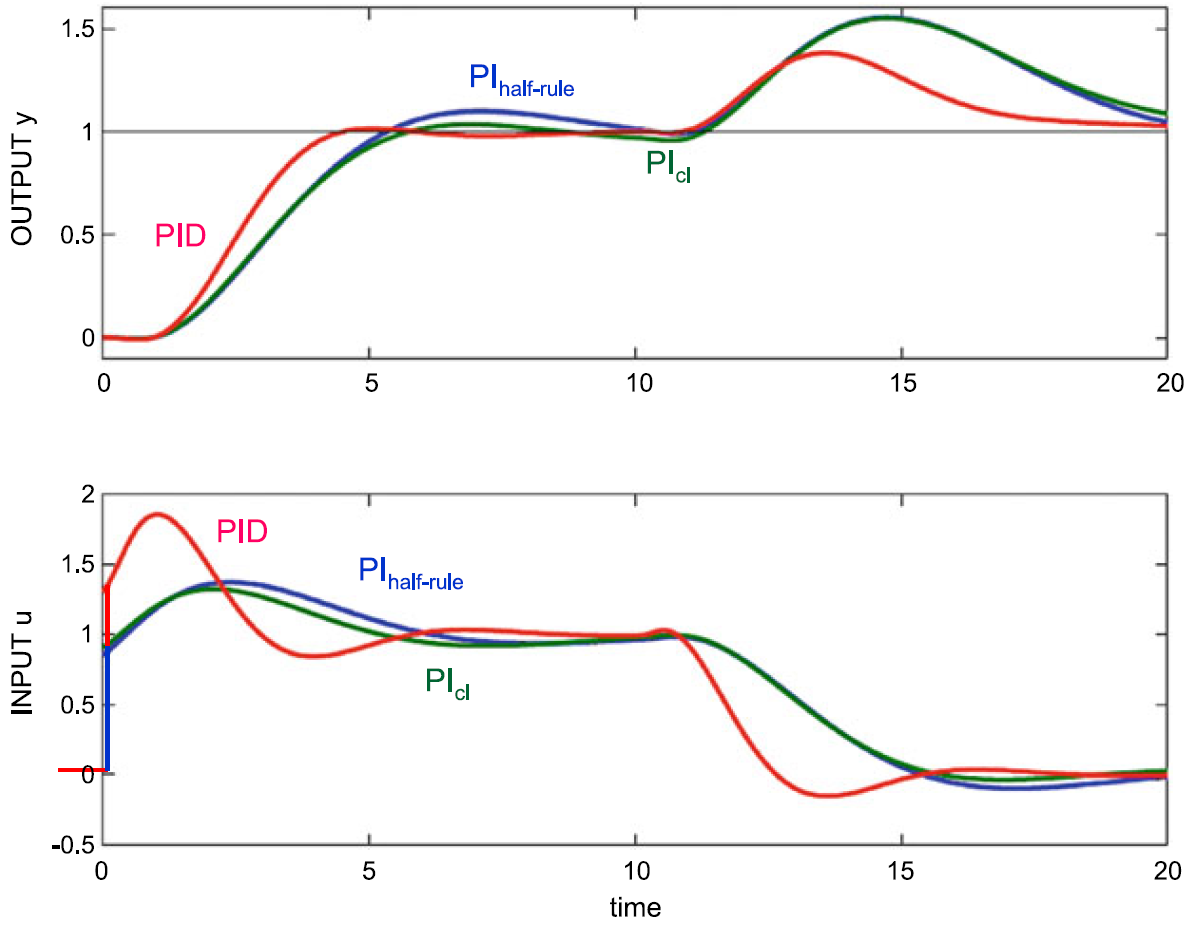
The top graph shows the measured process variable (the process’s output); the bottom graph shows the controller output (the process’s input). The setpoint is changed at t=0, and the external process load is changed at t=10. The PID control’s D-action is on the process variable only, not on the setpoint. The PID control action is fast and accurate; the PI-only actions keep the valve movements smaller.[1]
PID controller responds to diverse needs
…proportional-integral-derivative (PID) is by far the dominant feedback control algorithm.[2]
PID controllers are found in large numbers in all industries. The PID controller is a key part of systems for motor control. They are found in systems as diverse as CD and DVD players, cruise control for cars, and atomic force microscopes. The PID controller is an important ingredient of distributed systems for process control.[3]
There are approximately three million regulatory controllers in the continuous process industries…
Based on a survey of… controllers in the refining, chemicals and pulp and paper industries… 97% of regulatory controllers utilize a PID feedback control algorithm.[2]
Many sophisticated control strategies, such as model predictive control, are also organized hierarchically. PID control is used at the lowest level; the multivariable controller gives the set points to the controllers at the lower level.
The PID controller can thus be said to be the “bread and butter” of control engineering.[3]
PID controller responds to error with proportional action
PID controllers are defined by the control algorithm, which generates an output based on the difference between setpoint and process variable (PV). That difference is called the error…
…the most basic controller would be a proportional controller. The error is multiplied by a proportional gain and that result is the new output.
When the error does not change, there is no change in output. This results in an offset for any load beyond the original load for which the controller was tuned. A home heating system might be set to control the temperature at 68˚F. During a cold night, the output when the error is zero might be 70%. But during a sunny afternoon that is not as cold, the output would still be 70% at zero error. But since not as much heating is required, the temperature would rise above 68˚F. This results in a permanent off-set.
PID controller responds to error footprint with integral action
Integral action overcomes the off-set by calculating the integral of error or persistence of the error.
This action drives the controller error to zero by continuing to adjust the controller output after the proportional action is complete. (In reality, these two actions are working in tandem.)
PID controller responds to projected change with derivative action
And finally, there is a derivative term that considers the rate of change of the error. It provides a “kick” to a process where the error is changing quickly…
Derivative action is sensitive to noise in the error, which magnifies the rate of change, even when the error isn’t really changing. For that reason, derivative action is rarely used on noisy processes and if it is needed, then filtering of the PV is recommended.
Since a setpoint change can look to the controller like an infinite rate of change and processes usually change more slowly, many controllers have an option to disable derivative action on setpoint changes and instead of multiplying the rate of change of the error, the rate of change of the PV is multiplied by the derivative term.
Derivative is not often required, but can be helpful in processes that can be modelled as multiple capacities or second order.[4]
PID controller responds simply and intuitively
The PID controller is a simple implementation of feedback.
It has the ability to eliminate steady-state offsets through integral action, and it can anticipate the future through derivative action.[3]
- Skogestad, Sigurd, and Chriss Grimholt. “The SIMC method for smooth PID controller tuning.” PID Control in the Third Millennium. Springer London, 2012. 147-175.
- Desborough, Lane, and Randy Miller. “Increasing customer value of industrial control performance monitoring-Honeywell’s experience.” AIChE symposium series 326 (2002): 172-192.
- Åström, Karl Johan, and Tore Hägglund. Advanced PID control. ISA-The Instrumentation, Systems and Automation Society, 2006, p. 1.
- Heavner, Lou. “Control Engineering for Chemical Engineers.” Chemical Engineering 124.3 (Mar. 2017): 42-50.